8.1. Theory

8.1.1. Synthesis of Propylene Oxide

Corrosive propylene oxide is the simplest chiral epoxide and of great industrial importance. The historically most important synthesis is based on hydrochlorination and ring closure of the resulting chloropropanols in a basic environment:

Fig. 8.1 Epoxide reaction.

The resulting epoxide is most often directly used as a racemate.

Exercise 1

What kind of reaction mechanism would you expect? Would you expect the stereochemistry at the chiral carbon to be preserved? Identify the chirality centre in the chloropropanoate and the product epoxide.

Exercise 2

Suggest possible transition state structures.

8.1.2. Transition State Theory

Any chemical reaction is nothing but a mere rearrangement of nuclei, and all the possible ways the nuclei could rearrange span a plethora of possible paths. Hence, there are usually many paths on the potential energy surface (PES) that connect reactants and products, and depending on the energy of the system, more or less of these paths will be accessible for the chemical transformation. Finding all of these paths is a daunting task, as all the involved degrees of freedom have to be mapped out of the full PES onto a reduced - but still multidimensional - PES. The study of these rare events using various mapping techniques is an involved subject; various elaborate techniques exist for elucidating possible paths. They are, however, often linked to computationally expensive molecular dynamics simulations (MD) and are more concerned with studying the free energy surface (FES; including entropic effects) rather than just the PES. For the study of the latter, simpler models exist, often yielding a qualitatively sufficient picture to explain many chemical transformations.

8.1.3. A Minimum (Potential) Energy Path

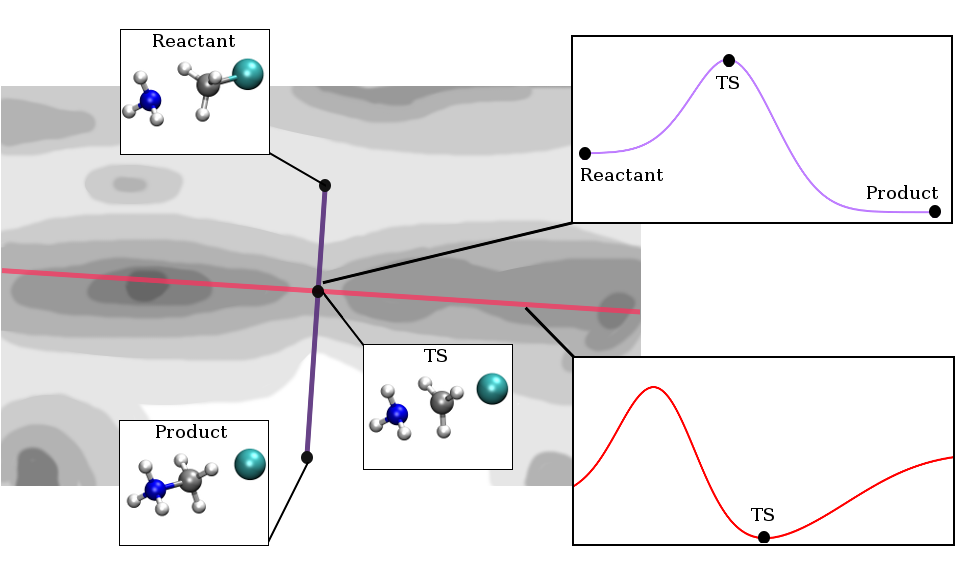
Fig. 8.2 Visualisation of transition state theory in a ficticious 2D PES. Dark areas correspond to high-energy regions, whereas brightly coloured areas correspond to energetically lower lying states. Reactants and products are connected through a minimum energy path via a first-order saddle point, the transition state.

The fundamental concepts that greatly simplify the problem of finding reactive pathways on the PES were introduced as early as the nineteenth century, and in the 1930ies, their development culminated in a model called Transition State Theory. Assuming that the most likely path is also the unique path by which a reaction proceeds, one searches for the minimum energy path connecting reactants and products along the reaction coordinate. The energetically highest point along this path is a stationary point, the transition state (cf. figure 2). There is a striking analogy with lazy hikers that want to get from one valley to another: They will not choose the steepest path across a peak of 4000 m altitude, but they will rather choose a mountain pass (a col) to reach their destination with least effort. The villages in the valleys correspond to reactant and product states: In all directions, the path goes uphill.
It is straightforward to see from this analogy that the transition state is given by a first order saddle point. Along all possible coordinates except the reaction coordinate, the potential energy surface goes uphill; along the reaction coordinate, it goes downhill. This implies that the transition state is the highest energy point along the reaction coordinate, but the lowest energy point perpendicular to the reaction coordinate. This gives raise to the typical transition state diagrams that are frequently used to describe simple reactions in organic chemistry.

8.1.4. From Curvature to Vibrational Frequencies: The Hessian

(Local) Minima and saddle points of any order are all stationary points, stable points on the potential energy surface where the curvature is zero. This implies that the first derivative matrix of the nuclear coordinates vanishes at any stationary point. However, this information will not be sufficient to classify the nature of the stationary point. The matrix of second derivatives, the Hessian, has to be used instead. The Hessian matrix can be diagonalised, and the resulting eigenvalues contain the desired information on the stationary point: If all eigenvalues are negative, the corresponding geometry constitutes a local maximum; if they are all positive, the geometry corresponds to a local minimum. If positive and negative eigenvalues occur, one is dealing with an N\(^{th}\) order saddle point. The task of finding a transition state using the Hessian matrix of the system is therefore easy: One searches for the geometry that yields a Hessian with exactly one negative eigenvalue, i.e. a first-order saddle point - the transition state. (Similarly, the eigenvalue test can also be used to check whether a geometry optimisation has found a true minimum, or whether it is blocked in a flat region of the PES.)
The Hessian of the system contains further useful information. For instance, in the approximation of a harmonic oscillator in a quadratic potential, the vibrational eigenvalues are known:

\[\begin{aligned} E_\nu = \left(\nu+\frac{1}{2}\right)\hbar\omega \quad ; \quad \omega = \sqrt{\frac{k}{m}},\end{aligned}\]

where \(k\) is a force constant and \(m\) is the (reduced) mass of the oscillator. By locally approximating the PES to be harmonic, the (decoupled) vibrational frequencies for the corresponding geometries can be calculated from the Hessian matrix: It turns out that \(k\) is simply given by the eigenvalues of the Hessian evaluated in mass-weighted coordinates. For equilibrium geometries with positive Hessian eigenvalues, the molecular vibrational frequencies \(\omega\) (as observed in IR spectroscopy) can easily be calculated, and the corresponding vibrational modes can be visualised. The possiblity of visualising the frequencies opens up a valuable tool in the transition state search: As a first order saddle point will have one negative eigenvalue, the corresponding frequency will be imaginary. By visualising this imaginary frequency, one can immediately verify whether one has found a TS of interest, or just another, non-relevant first-order saddle point on the TS: If the imaginary vibrational node corresponds to a motion that transfers reactants to products, the search was successful.