2.1. Basis Sets - Defining Vector Spaces

Three questions have to be addressed before tackling an electronic structure problem:

1. Which computer code is best suited for a given problem

2. Which computational method will give the most accurate results in a reasonable time

3. What basis set offers the best compromise of accuracy and efficiency?

Throughout this course, you shall always be using the same code (Psi4) - but you will get to try out some of the different approaches discussed in the lecture. Before the first practical example - applying the Hartree-Fock-Roothaan scheme (that you will treat in detail in the lectures) to simple systems, there remains one issue to be resolved: What is the basis in which we want to expand our wavefunction that is described by the in principle infinite expansion

(2.1)\[ \Psi(\mathbf{r}_1,\dots,\mathbf{r}_N) = \sum_j c_j \psi_j(\mathbf{r}_1,\dots,\mathbf{r}_N) \]

2.1.1. One-Electron Wavefunctions: Slater-Type Orbitals (STOs)

By defining a basis set, we define a vector space in which the Schrödinger equation is to be solved - and we wish this space to be as close as possible to the complete space that defines the accurate solution. You have already seen that the Hartree-Fock scheme makes a convenient (but not always accurate) approximation to \(\Psi\), in that it is assumed that one Slater determinant is enough to accurately describe the problem. Therefore, in Hartree-Fock theory, the (2.1) reduces to:

(2.2)\[ \Psi(\mathbf{r}_1,\dots,\mathbf{r}_N) = \psi(\mathbf{r}_1,\dots,\mathbf{r}_N), \]

where

(2.3)\[ \psi(\mathbf{r}_1,\dots,\mathbf{r}_N) = \det\left|\phi_1(\mathbf{r}_1),\dots,\phi_N(\mathbf{r}_N)\right| \]

is a Slater determinant to account for the antisymmetry requirement as discussed in the preceeding chapter, and the \(\left\{\phi\right\}\) are one-electron orbitals. Although an expression for the many-electron wavefunction in terms of one-particle wavefunctions is now given, the latter are not yet specified. An intuitive approach to the one-electron orbitals may be based on the LCAO (Linear Combination of Atomic Orbitals) theory, where one-particle molecular orbitals are formed from one-particle atomic orbitals. This implies that \(\phi_m(\mathbf{r}_m)\) will be expanded in terms of all atomic one-particle orbitals of the system, a set of atomic basis functions

(2.4)\[ \phi_m(\mathbf{r}_m) = \sum_n D_{mn} \chi_n(\mathbf{r}_m), \]

where the \(\left\{\chi\right\}\) are the atomic orbitals and \(D_{mn}\) is the expansion coefficient (the contribution) of the n\(^{th}\) atomic orbital to the single-particle molecular orbital \(\phi_m\). As the Hartree-Fock many-electron wavefunction is expressed as a single Slater determinant, the coefficients \(c_j\) as defined in the introduction vanish, and the only coefficients left in the definition are the \(D_{mn}\). These are the expansion coefficients that are optimised in a Hartree-Fock calculation.

Still, the question how to define the single-particle atomic orbitals is not yet resolved. In principle, the condition that there be a cusp at the nuclei and that the orbital fall off exponentially at large distances from the nuclei dictates a certain form. One suitable form was proposed by Slater in the 30ies of the last century:

(2.5)\[ \chi_{\xi,n,l,m}(\mathbf{r},\theta,\phi) = N \cdot Y_{lm}(\theta,\phi)\cdot r^{n-1}\cdot e^{-\zeta r} \]

A Slater-type orbital is composed of an angular part that is taken from the exact solution of the hydrogen atom \(Y_{lm}\) (the spherical harmonics), an exponential part (to ensure the right long-range decay) and a polynomial. However, products of these functions will need to be evaluated - and these are impractically expensive to compute. It is therefore more convenient to choose basis functions that offer some computational advantages. Gaussian functions would be especially suited, as products of Gaussians will simply yield another Gaussian that is placed off the initial centres. Frank Boys therefore proposed to approximate Slater-type orbitals with a linear combination of Gaussian-type functions. These Gaussian-type basis functions are referred to as contraction functions. This implies that the atomic basis function \(\chi\) is in turn defined by several basis functions (the term contraction is chosen to avoid confusion between the atomic basis functions, and the linear combination of Gaussians they are based upon):

(2.6)\[ \chi_{\xi,n,l,m}^{STO-3G}(\mathbf{r},\theta,\phi) = \sum_{i=1}^3 d_i \cdot N_i \cdot Y_{lm}(\theta,\phi) \cdot r^{2n-2-l} \cdot e^{-\xi_i r^2}, \]

where \(N_i\) is a normalisation constant, and \(\xi_i\) is the i\(^{th}\) prefactor in the exponent that guarantees an optimal fit to the Slater-type orbitals. This defines a minimal Gaussian basis set known as STO-3G (STO stands for Slater-type orbital and refers to the origin of the Gaussian expansion). The term minimal basis does not refer to the number of contractions, but to the number of basis functions: For each orbital, there is one basis function. Minimal bases create minimal computational overhead, but will often not provide sufficient flexibility to accurately describe the system’s wavefunction - there is always a certain trade-off between the desired accuracy and the efficiency of a calculation. For more details, you may refer to the main course script.

2.1.1.1. Pople-Type Split-Valence Basis Sets

Core and valence orbitals are equally important for the energetics of a system, but bonding is dictated by the valence electrons. One may therefore want to improve over the STO-3G basis by allowing for additional flexibility in the description of valence electrons. In a split-valence basis set, the number of basis functions that is assigned to core orbitals differs from the one for the valence orbitals. Usually, core electrons are described by one function, which is in turn composed of a certain number of Gaussian functions (i.e. contractions). For the description of the valence electrons, multiple functions will be included (most often 2 to 6); and every of these functions will in turn be expressed by a varying number of Gaussian contractions.

An example of a split-valence basis set is John Pople’s 3-21G. The notation encodes information about the contraction: The number on the left of the hyphen denotes the number of contractions for the core orbitals, which consist of a single basis function per orbital only. The information on the right describes the contraction of the valence orbitals: There are two numbers, hence there are two basis functions \(\chi\) per orbital. These basis functions, in turn, are constructed by two and one Gaussian contraction(s) respectively.

Fig. 2.1 Explanation of what the numbers in the 3-21G basis set notation mean.

Consider, as a practical example, carbon with the electronic configuration \(1s^22s^22p^2\) in the 3-21G basis. The core orbital (1s) is given by a contraction over three Gaussians.

(2.7)\[ \chi(1s)=\sum_{k=1}^3 \alpha_{1s,k}\mathrm{e}^{-\zeta_{1s,k}\mathbf{r}^2} \]

To every valence orbital (2s and 2p), one function containing two Gaussians and one function containing one Gaussian is attributed.

(2.8)\[\begin{split} \begin{aligned} \begin{split} \chi(2s)^{(2)} & = \sum_{k=1}^2 \alpha_{2s,k} \ \mathrm{e}^{-\zeta_{2s,k}\mathbf{r}^2} \\ \chi(2s)^{(1)} & = \alpha'_{2s} \ \mathrm{e}^{-\zeta'_{2s}\mathbf{r}^2} \end{split} \end{aligned} \end{split}\]

(2.9)\[\begin{split} \begin{aligned} \begin{split} \chi(2p)^{(2)}_{\Gamma} & = \sum_{k=1}^2 \alpha_{2p,k} \ \Gamma_p(\mathbf{r}) \ \mathrm{e}^{-\zeta_{2p,k}\mathbf{r}^2} \\ \chi(2p)^{(1)}_{\Gamma} & =\alpha'_{2p} \ \Gamma_p(\mathbf{r}) \ \mathrm{e}^{-\zeta'_{2p}\mathbf{r}^2} \end{split} \end{aligned}\end{split}\]

where \(\Gamma_p(\mathbf{r})=x,y,z\) accounts for orbitals \(p_x\), \(p_y\), \(p_z\). Fixed coefficients are added in front of each Gaussian, denoted by \(\alpha\).
For each atom, there are individual sets of parameters \(\alpha\) and \(\zeta\), which were determined back when the basis set was designed. These contraction parameters are never changed during an electronic structure calculation. Recall that the molecular one-electron wavefunctions are variable linear combinations of fixed atomic orbitals; changing the contraction parameters during the calculation would change and therefore mess up the atomic basis functions. The values for standard basis sets are usually hard-coded in the electronic structure codes.

For instance, Psi4 represents the basis set parameters in the following format:

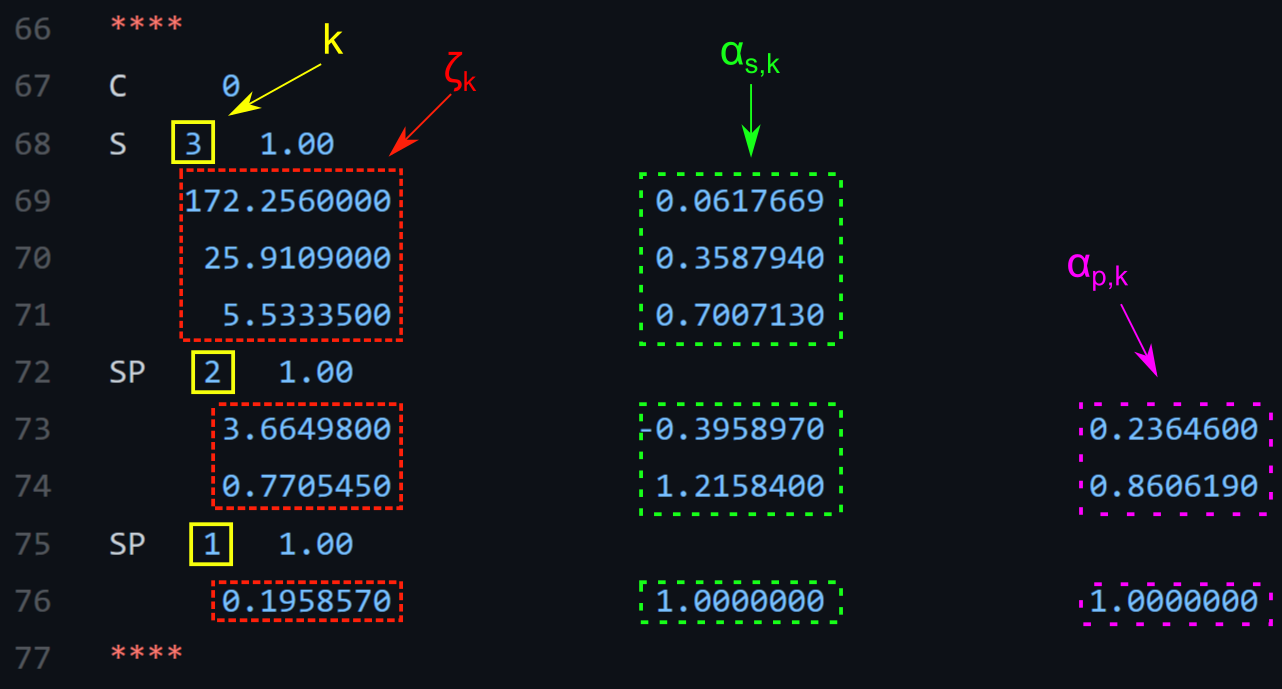
Fig. 2.2 Example of a basis set parameter file

which are the 3-21G basis set parameters for a carbon atom (from psi4/psi4).
The \(S\) entry contains information about the core, the \(SP\) entries about the valence orbitals. The first number after \(S\) or \(SP\) refers to the index of the contraction \(k\), the column below gives the contraction parameters \(\zeta_k\), the second column gives the \(\alpha_{s,k}\) and the third the \(\alpha_{p,k}\). Note that if there is just one contraction, then \(\alpha_{l,1} = 1\). In general, s and p orbitals do not differ in \(\zeta_k\), but just in \(\alpha_{l,k}\).

Exercise 1

A minimal basis set…
a) …always gives the lowest energy.
b) …is optimized for small molecules.
c) …contains one basis function for each atomic orbital only.

Exercise 2

A split-valence basis set…
a) …contains two basis functions for each valence atomic orbital.
b) …doubles the CPU time of the calculation.
c) …attributes a different number of basis functions to valence and core orbtials.

Exercise 3

Which of the following basis sets does not contain polarisation functions?
a) 6-31G\(^\ast\)
b) 6-31G(d,p)
c) 3-21+G
d) DZP

Exercise 4

Diffuse functions are added to a basis set to…
a) …save CPU time.
b) …better represent electronic effects at larger distances from the nuclei.
c) …take polarisation into account.
d) …enhance the description of core orbitals.

Exercise 5

Using the information given about the 3-21G contraction coefficients:
a) Give the basis functions corresponding to the 1s, 2s and 2p orbitals of Carbon (Hint: use information from Fig. 2.2 ).
b) If you wish to calculate the Hartree-Fock energy of a carbon atom, how many coefficients are optimised during the calculation?

Exercise 6

You wish to calculate the wavefunction of ethylene C\(_2\)H\(_2\) using the 6-31G* basis.
Indicate the number of basis functions and the number of Gaussian primitives that will be used in the calculation.