8.2. Locating Transition States: Constrained Optimisations#
Unlike a geometry optimisation, a transition state search requires more than just some guess. Finding the transition state from a reactant or a product structure will be computationally unfeasible, as those structures are given by local minima on the PES. Hence, all possible paths originating from these minima will go uphill (recall the mathematical definition of a minimum with respect to its derivatives), and it cannot be clear in advance which paths will actually connect reactants and products, or which path(s) will proceed via the lowest lying transition state. Instead, one needs a guess that is reasonably close to the real transition state, such that the curvature of the potential energy surface close to the TS is known, making it possible to proceed uphill along the reaction coordinate until the transition state is reached. The general procedure for a transition state search includes the construction of a guess geometry that should be reasonably close to the expected TS, followed by a constrained optimisation (cf. figure 3).
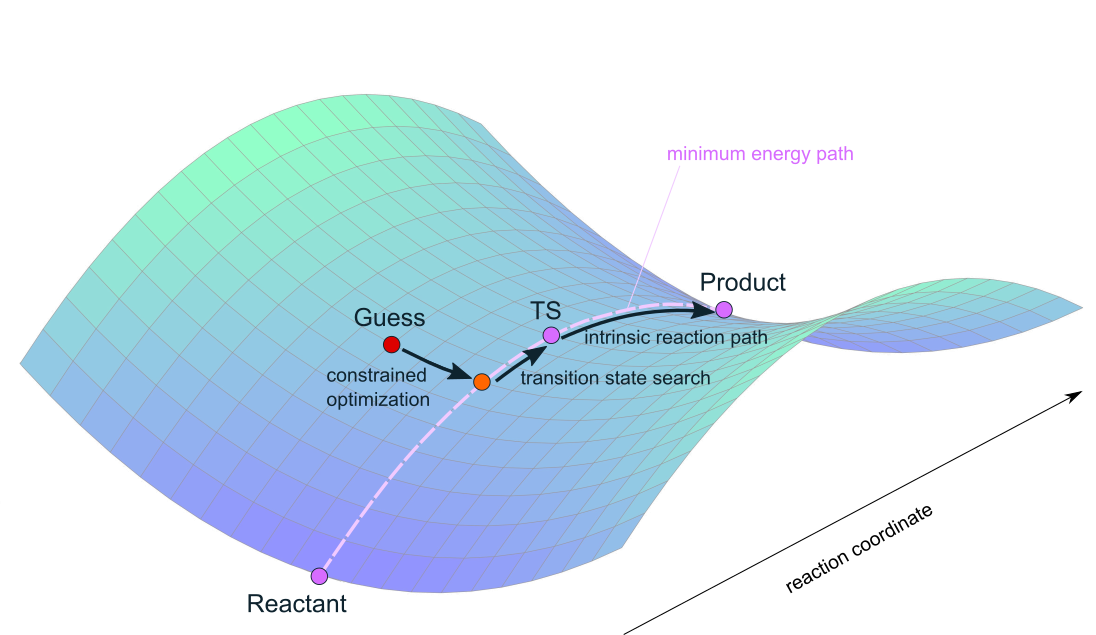
Fig. 8.3 Finding a transition state from an initial guess by performing a constrained optimisation followed by a TS search.#
In a constrained optimisation, all degrees of freedom which are not deemed relevant for the reaction are relaxed, whereas the relevant degree(s) of freedom is (are) kept fixed. After the optimisation, the curvature of the PES is evaluated at the chosen geometry (either analytically or numerically, cf. the following section). If the constrained degree(s) of freedom was (were) suitably chosen, the paths associated to the unconstrained N-1 degrees of freedom will go uphill in both directions, indicating that the corresponding structural parameters were properly relaxed. There should be one degree of freedom remaining that is associated to a path that goes downhill on one side and uphill on the other side: This will be the path that leads uphill to the transition state. As the associated degree of freedom is then known, the geometry can then be optimised to a transition state by selectively ‘walking uphill’ along this specific path.
8.2.1. Constructing a Guess#
You can find below the Z-matrix for the chloropropanolate (2-Chloro-1-propanol) already set, obtained using the Open Source Software Avogadro. We want to set the Z-matrix for the transition state editing this matrix. Correct the parameters adapting the conformation to be reasonably close to the transition state: for the TS, one expects that the C-Cl bond will already be elongated, whereas the oxygen atom will start to form the epoxide ring. Change the bond angle of the oxygen atom to something smaller than the original value, such as 80◦, and modify the bond length for the C-Cl bond to an elongated conformation, such as 2.40 Å. Moreover, you need to delete the hydrogen bond to the oxygen atom, and edit the Z-matrix accordingly.
import psi4
import py3Dmol
import numpy as np
import matplotlib.pyplot as plt
psi4.set_num_threads(2)
psi4.set_memory('2 GB')
import sys
sys.path.append("..")
from helpers import *
Threads set to 2 by Python driver.
Memory set to 1.863 GiB by Python driver.
#Z-matrix for the chloropropanolate
chloropropanolate = psi4.geometry("""
0 1
symmetry c1
c
c 1 cc2
cl 1 clc3 2 clcc3
h 1 hc4 2 hcc4 3 dih4
c 1 cc5 2 ccc5 3 dih5
o 2 oc6 1 occ6 3 dih6
h 2 hc7 1 hcc7 6 dih7
h 2 hc8 1 hcc8 6 dih8
h 5 hc9 1 hcc9 2 dih9
h 5 hc10 1 hcc10 9 dih10
h 5 hc11 1 hcc11 9 dih11
h 6 ho 2 hoc2 1 dih12
cc2 = 1.500000
clc3 = 1.790000
clcc3 = 109.471
hc4 = 1.089000
hcc4 = 109.471
dih4 = 100.000
cc5 = 1.500000
ccc5 = 109.471
dih5 = -100.000
oc6 = 1.430000
occ6 = 110.600
dih6 = 180.000
hc7 = 1.070000
hcc7 = 109.471
dih7 = 120.000
hc8 = 1.070000
hcc8 = 109.471
dih8 = 240.000
hc9 = 1.070000
hcc9 = 109.471
dih9 = 180.000
hc10 = 1.070000
hcc10 = 109.471
dih10 = 120.000
hc11 = 1.070000
hcc11 = 109.471
dih11 = 240.000
ho = 0.97
hoc2 = 109.471
dih12 = 180.0
""")
#Edit the Z-matrix to obtain the TS guess according to the requests above
ts_guess = psi4.geometry("""
0 1
symmetry c1
c
c 1 cc2
cl 1 clc3 2 clcc3
h 1 hc4 2 hcc4 3 dih4
c 1 cc5 2 ccc5 3 dih5
o 2 oc6 1 occ6 3 dih6
h 2 hc7 1 hcc7 6 dih7
h 2 hc8 1 hcc8 6 dih8
h 5 hc9 1 hcc9 2 dih9
h 5 hc10 1 hcc10 9 dih10
h 5 hc11 1 hcc11 9 dih11
h 6 ho 2 hoc2 1 dih12
cc2 = 1.500000
clc3 = 1.790000
clcc3 = 109.471
hc4 = 1.089000
hcc4 = 109.471
dih4 = 100.000
cc5 = 1.500000
ccc5 = 109.471
dih5 = -100.000
oc6 = 1.430000
occ6 = 110.600
dih6 = 180.000
hc7 = 1.070000
hcc7 = 109.471
dih7 = 120.000
hc8 = 1.070000
hcc8 = 109.471
dih8 = 240.000
hc9 = 1.070000
hcc9 = 109.471
dih9 = 180.000
hc10 = 1.070000
hcc10 = 109.471
dih10 = 120.000
hc11 = 1.070000
hcc11 = 109.471
dih11 = 240.000
ho = 0.97
hoc2 = 109.471
dih12 = 180.0
""")
drawXYZSideBySide_labeled(chloropropanolate, ts_guess)
Exercise 3
Include a screenshot of the transition state in your report that you obtained and the corresponding Z-matrix for the transition state guess
8.2.2. Constrained optimization#
We will first optimize our transition state guess keeping the C-Cl distance fixed.
ts_guess_opt = ts_guess.clone()
psi4.core.set_output_file(f'poxide.log', False)
psi4.set_options({"frozen_distance":"1 3"})
psi4.optimize('b3pw91/6-31+G*', molecule=ts_guess_opt)
drawXYZSideBySide_labeled(ts_guess, ts_guess_opt)
8.2.3. Finding the Transition State#
Now that we have our transition state guess optimized, we want to find out whether this guess is close to the transition state (meaning it has one imaginary frequency) and then optimize to the actual transition state.
If we set full_hess_every to 0, a frequency calculation will be performed at the begining (you could also do it seperately using psi4.frequency([..]). By setting opt_type to ts the optimization will try to find the 1st order saddlepoint that is the transition state.
We will write the normal modes to a file for visualization.
ts = ts_guess_opt.clone()
psi4.core.clean_options()
psi4.core.set_output_file(f'ts.log', False)
psi4.set_options({
"opt_type":"ts",
"geom_maxiter":500,
"normal_modes_write": True,
"full_hess_every":0 #0 compute the initial Hessian only
})
E = psi4.optimize('b3pw91/6-31+G*', molecule=ts)
#print out TS in case something goes wrong
with open('ts.xyz', 'w') as f:
f.write(ts.save_string_xyz_file())
We can also compare the TS with the guess to see how far we are.
drawXYZSideBySide_labeled(ts_guess_opt, ts)
Exercise 4
Take a screenshot of the optimised transition state structure. How did the structure change with respect to the constrained-optimised guess?
We can now have a look at the normal model that we obtained, for that we need to first check how the file is named. Then you can visualize one normal mode at time.
# check how the file is named, this is a bash command
# ls means list all the files in the current directory
# -ltrh are flags that print output as a detailed list (-l) in reversed order(-r) by time (-t) with human readable units (-h)
!ls -lrth ts.*.molden_normal_modes
# be sure to use the right file in the show_normal_modes
show_normal_modes(filename='FILENAME.XX.molden_normal_modes')
Exercise 4
Report the value of the negative frequency that you obtain. What motion is this mode related to? What motions are associated with low and high vibrational frequencies? Choose two positive vibrational modes and desribe their particular associated motion.
Exercise 5
Is the transition state you predicted an early or a late transition state? What about the guess?
Exercise 6
Having found a transition state, how would you now obtain the barrier height for your reaction? Are there ways of verifying whether you have found a meaningful transition state? Bonus: How would you define ‘meaningful’ in this context?
