6.1. Methylcyclohexane A-value

In this exercise we will compute the A-Value of the methyl group in a methylcyclohexane molecule. A-values are numerical values used in the determination of the most stable orientation of atoms in a molecule, derived from energy measurements of the different cyclohexane conformations of a monosubstituted cyclohexane chemical. In particular, we will compare a cyclohexane monosubstituted with a methyl group in equatorial or axial position.

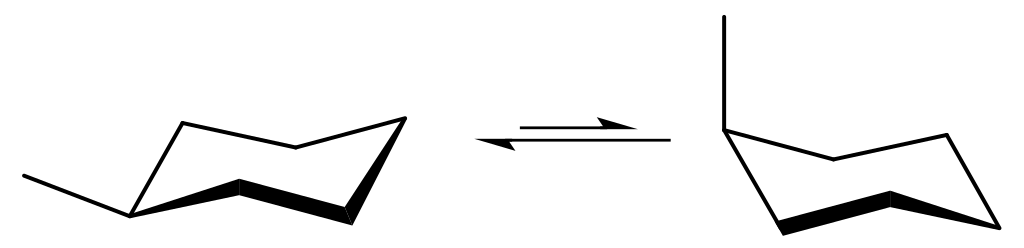
Fig. 6.1 Conformers considered to compute A-value for a methyl group. Image source

6.1.1. Creating the conformers

For larger molecules, the creation of an approximate xyz file that can be used as the molecular input coordinates is impossible. In these cases, one may refer to molecular visualization softwares.

Many different programs can be used for this task. Popular ones are for example Avogadro (open source, cross-plattform), MolView (https://molview.org/) (web-based), molden, GaussView (comes with the Gaussian quantum chemistry software), IQMol and many more.

An alternative is to download structures from a database such as PubChem. We will do this for methylcyclohexane in equatorial position.

Concerning the methylcyclohexane in axial position, for simplicity we provide you the coordinates below, but you could as well have drawn them yourselves. The coordinates need to be approximately right and many programs come with a force field optimization routine, that will quickly snap together all bonds to their equilibrium distances and so on.

import psi4
import pandas as pd

import sys
sys.path.append("..")

from helpers import *

psi4.set_num_threads(2)
psi4.set_memory('2 GB')

  Threads set to 2 by Python driver.

  Memory set to   1.863 GiB by Python driver.

2000000000

equatorial = psi4.geometry("pubchem:methylcyclohexane")

	Searching PubChem database for methylcyclohexane (single best match returned)
	Found 1 result(s)

axial = psi4.geometry("""
0 1
            C    -1.2274001186   0.0240644681   0.0713205260
            C    -0.4303137771   1.2916249494   0.4268585314
            C    -0.4722293117  -1.2264891935   0.5553779250
            C     1.0230602330   1.2466021870  -0.0584805092
            C     0.9810630014  -1.2793844777   0.0705620697
            C     1.7419564780  -0.0059874325   0.4503640869
            C    -1.5835089284  -0.0460222638  -1.4189886323
            H    -2.1693676159   0.0675361033   0.6153188260
            H    -0.4294212171   1.4082548027   1.5099113283
            H    -0.9316553296   2.1691116345   0.0246221983
            H    -1.0030678716  -2.1232152029   0.2435950228
            H    -0.4734758600  -1.2323353337   1.6446806077
            H     1.5465084148   2.1388141117   0.2762673484
            H     1.0547234511   1.2652076515  -1.1458128465
            H     1.0103574383  -1.4097971319  -1.0091493740
            H     1.4751656749  -2.1496795922   0.4954590794
            H     2.7555071747  -0.0428481064   0.0586760240
            H     1.8302774578   0.0479649801   1.5350921581
            H    -2.1583756764   0.8264696291  -1.7176644216
            H    -0.7081555279  -0.0931653015  -2.0577965825
            H    -2.1875114783  -0.9248063650  -1.6283284158
""")

drawXYZSideBySide(equatorial, axial)

You appear to be running in JupyterLab (or JavaScript failed to load for some other reason). You need to install the 3dmol extension:
jupyter labextension install jupyterlab_3dmol

Exercise 1

Why is it important to construct the starting structures in a specific conformation, although one is carrying out a geometry optimisation? Don’t we risk to end up in the same conformation after the optimization, since we are dealing in both cases with the same molecule, i.e. methylcyclohexane?

results_dict = {}

Hint

You can generate a table using python by creating a list of the methods you want to use and iterating over them. As we want to start the geometry optimizations from the same geometries it is important that you always optimize a clone of the original molecule. We can do this by using mol_to_optimize =  starting_mol.clone(). To display the table you need to store the results in a dictionary.

A dictionary in python looks like this: results_dict = {"key": "value"}. The value can be a str, int or even a list. In this case you can update the dictionary for each method iteration like so: results_dict[method] = [E1, E2, dH, label]

In the end you will have a full dictionary containing all the results which we can nicely print as a pandas dataframe using:

pd.DataFrame.from_dict(data, orient='index', columns=['E_reactant', 'E_product', 'ΔH(0K) [kcal/mol]', 'remark'])

psi4.core.set_output_file(f'a-val.log', False)

Exercise 2

Compute the energy of the two conformations and calculate the energy difference at 0 K, \(\Delta E_{0K} = E_{\text{axial}} - E_{\text{equatorial}}\), i.e. the A-value, filling the table below. Compare the results of different methods with the experimental value for the A-Value of the methil group in a methylcyclohexane molecule, 1.74 kcal/mol. For each method, use both 6-31+G* and 6-31+G** basis sets.

By adding %%time at the beginning of each cell, the execution time will be printed out. This quantity is related to the computational cost of the calculation and can help you to compare the different methods.

You can split up the calculations among yourselves to speed up the process.

Method	E_equatorial (Hartrees)	E_axial (Hartrees)	ΔE(0K) (kcal/mol)	Relative error %	Basis set	Remark (ψ /ρ based ?)	Wall time
HF
MP2
BLYP
MPW1PW91
B97-2
PBE
TPSS
M06-L
M06-2X
B3LYP-D3BJ
Reference	//	//	1.74	Experimental

%%time
methods =  [ ]  # add methods here
                # required methods:  'hf', 'mp2', 'blyp', 'mpw1pw91','b97-2','PBE', 'TPSS', 'M06-L', 'M06-2X', 'B3LYP-D3BJ'
                # required basis sets: '6-31+G*', '6-31+G**'
# clone molecules
equatorial_hf = equatorial.clone()
axial_hf = axial.clone()

for method in methods:
    product_dft = equatorial.clone()
    axial_dft = axial.clone()
    
    psi4.core.clean_options() # reset options for each run

    if method == "mp2": # for the mp2 method we will use the non-density fitted MP2 version which not the default in MP2
        psi4.set_options({'mp2_type':'conv'})
        
    # perform geometry optimizations and save into variables
    E_equatorial = None #
    E_axial = None #
    
    results_dict[method] = None # You can e.g use a list like this [E_equatorial, E_axial, ΔE_kcalmol,  "ρ/ψ based"]

# we insert the reference here
results_dict['reference'] = ['-','-', 1.74, 'exp']

# print out dictionary nicely 
# FYI: you can also print it to latex code by adding .to_latex() and using \usepackage{booktabs}
pd.DataFrame.from_dict(results_dict, orient='index', columns=['E_equatorial', 'E_axial', 'ΔE(0K) [kcal/mol]', 'remark'])

Exercise 3

What kind of basis sets were used for ψ based calculations? On which atoms will polarization and diffuse functions be included? Are we close to the basis set limit? Why, or why not?

Exercise 4

Comment on the performance of the wavefunction based methods and DFT, comparing both accuracy and computational time.

Can you imagine why some DFT methods perform better than others? How does DFT compare to MP2 and HF? Would you expect the exchange-correlation functionals to give similar errors in different systems?

An often cited target for the development of exchange-correlation functionals is an error below chemical accuracy, i.e. within 1 kcal mol \(^{-1}\) of the accurate result. Explain the accuracy of the results also in light of this.